当前位置：考研数学知识点——多元函数微分学
发布时间：2018-08-15 阅读量：
数学看似一个逻辑性很强的学科，但却非常的抽象，有时候一个概念会需要理解很久。今天我们要学的一个比较难的知识点叫多元函数微分学，微分比积分本就比较抽象且不好理解，还涉及到多元，快跟着小编复习巩固一下吧。
1、导数和微分到底是什么？
导数和微分其实就是数学家创造的两个代数工具，是为了从代数的角度来描述函数图像在几何上的变化。
说白了，就是每次描述函数图像变化，不用再画图了，有了这个，直接用算式算算就行了。因此导数和微分也是沟通几何和代数的重要桥梁之一。
而导数描述的是函数在一点处的变化快慢的趋势，是一个变化的速率；微分描述的是函数从一点（移动一个无穷小量）到另一点的变化幅度，是一个变化的量。
2、函数的变化
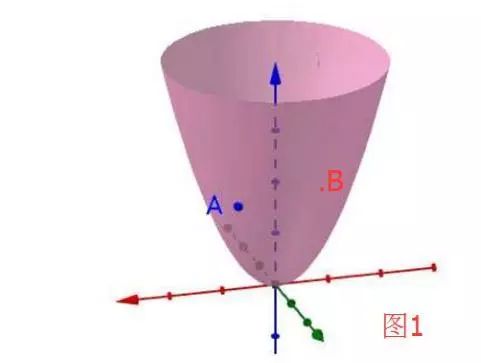
描述函数的变化，一个是描述函数的变化快慢，一个是描述函数变化多少。比如图1中，类似于一元函数的探讨，想知道函数在A点变化的快慢趋势，以及从A点到B点变化的幅度是多少。
另外我们多元函数的图像还有一个有意思的问题，就是函数可以固定一个变量，让另一个变量来变化，那么这又是与一元函数的十分不同的变化了，其实这是一个变化维度的问题。
►多元函数的变化，要考虑哪些问题：
（1）函数在A点的趋势变化。
（2）函数从A到B的变化的量。
（3）函数降维时候的变化，比如固定y，将二元函数看成一个一元函数来让x单独变化，又会产生什么变化。
3、多元函数的相关概念
明确了我们要考虑的问题，其实就是怎么用数学工具来描述上面的那些变化，就要动手来解决问题了。如何将一元函数的导数和微分的知识进行相应的拓展，于是就产生了多元函数微分学的那些概念。
（1）方向导数：本质就是函数在A点无数个切线的斜率的定义。每一个切线都代表一个变化的方向。
（2）梯度：函数在A点无数个变化方向中变化最快的那个方向。
（3）全微分：函数从A点到B点变化的量（其实是取一个无穷小的变化的量）。
（4）偏导：多元函数降维时候的变化，比如二元函数固定y，只让x单独变化，从而看成是关于x的一元函数的变化来研究。
微信公众号
微博二维码