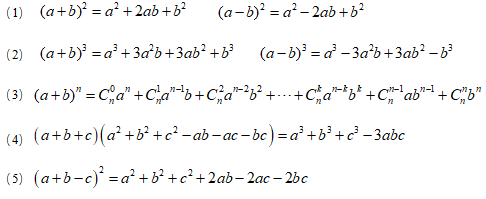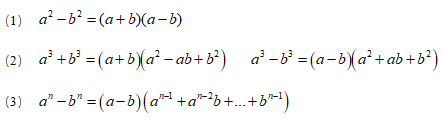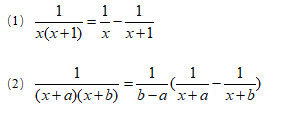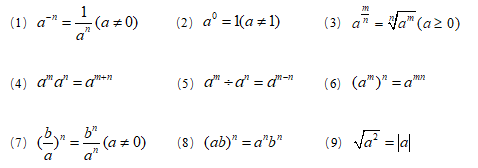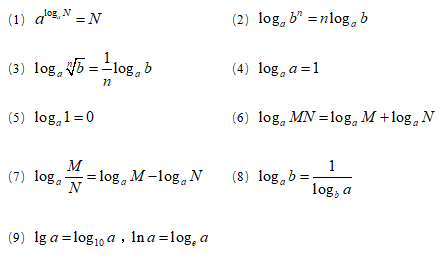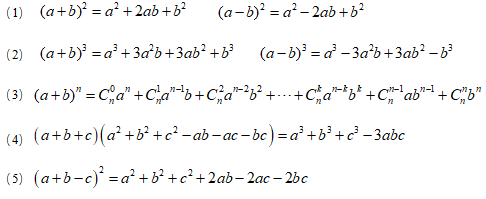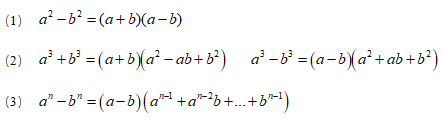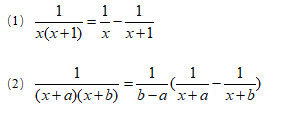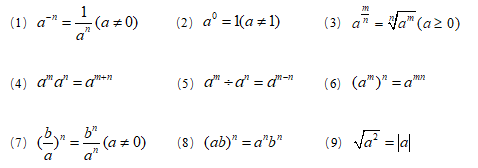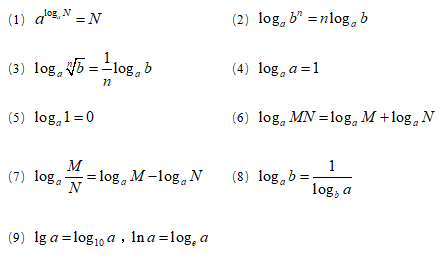当前位置：管综数学 | 常用公式、定理及易错点大全
发布时间：2021-01-23 阅读量：
数学四大部分包括算术、代数、几何、数据分析。很多考研er们在答题时，不知道从哪里下手，就是因为对这四部分的公式不熟悉！
今天我们就一起盘点一下管综数学常用公式！要求同学们能做到熟练掌握，灵活运用哟~
一、常用公式大盘点
1.乘法公式与二项式定理
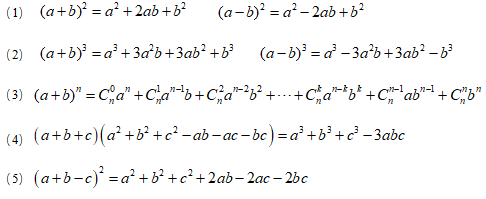
2.因式分解
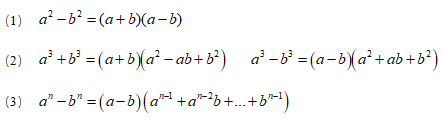
3.分时裂项
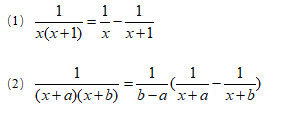
4.指数运算
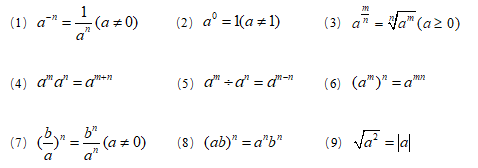
5.对数运算
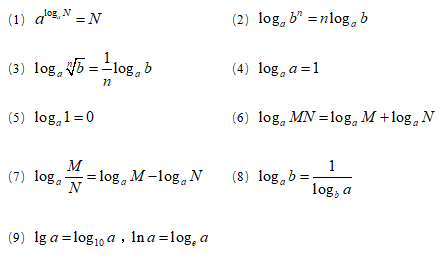
6.函数
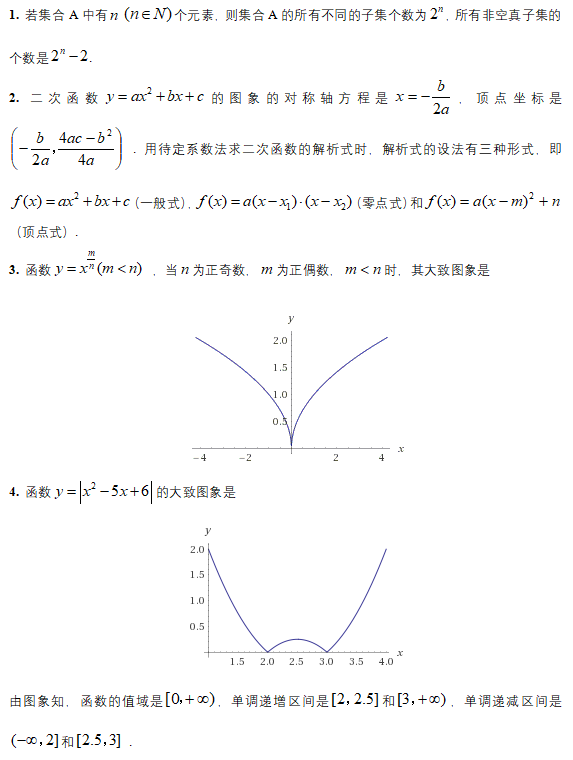
7.不等式
8.数列
9.排列组合、二项式定理
10.新析几何
11.立体几何
二、常用定理大盘点
1.过两点有且只有一条直线。
2.两点之间线段最短。
3.同角或等角的补角相等。
4.同角或等角的余角相等。
5.过一点有且只有一条直线和已知直线垂直。
6.直线外一点与直线上各点连接的所有线段中，垂线段最短。
7.平行公理 经过直线外一点，有且只有一条直线与这条直线平行。
8.如果两条直线都和第三条直线平行，这两条直线也互相平行。
9.同位角相等，两直线平行。
10.内错角相等，两直线平行。
11.同旁内角互补，两直线平行。
12.两直线平行，同位角相等。
13.两直线平行，内错角相等。
14.两直线平行，同旁内角互补。
15.定理：三角形两边的和大于第三边。
16.推论：三角形两边的差小于第三边。
17.三角形内角和定理：三角形三个内角的和等于180°。
18.推论1：直角三角形的两个锐角互余。
19.推论2：三角形的一个外角等于和它不相邻的两个内角的和。
20.推论3：三角形的一个外角大于任何一个和它不相邻的内角。
21.全等三角形的对应边、对应角相等。
22.边角边公理(sas)：有两边和它们的夹角对应相等的两个三角形全等。
23.角边角公理( asa)：有两角和它们的夹边对应相等的两个三角形全等。
24.推论(aas)：有两角和其中一角的对边对应相等的两个三角形全等。
25.边边边公理(sss)：有三边对应相等的两个三角形全等。
26.斜边、直角边公理(hl)：有斜边和一条直角边对应相等的两个直角三角形全等。
27.定理1：在角的平分线上的点到这个角的两边的距离相等。
28.定理2：到一个角的两边的距离相同的点，在这个角的平分线上。
29.角的平分线是到角的两边距离相等的所有点的集合。
30.等腰三角形的性质定理：等腰三角形的两个底角相等 (即等边对等角)。
31.推论1：等腰三角形顶角的平分线平分底边并且垂直于底边。
32.推论2：等腰三角形的顶角平分线、底边上的中线和底边上的高互相重。
33.推论3 等边三角形的各角都相等，并且每一个角都等于60°。
34.等腰三角形的判定定理 如果一个三角形有两个角相等，那么这两个角所对的边也相等(等角对等边)。
35.推论1：三个角都相等的三角形是等边三角形。
36.推论2：有一个角等于60°的等腰三角形是等边三角形。
37.在直角三角形中，如果一个锐角等于30°那么它所对的直角边等于斜边的一半。
38.直角三角形斜边上的中线等于斜边上的一半。
39.定理：线段垂直平分线上的点和这条线段两个端点的距离相等。
40.逆定理：和一条线段两个端点距离相等的点，在这条线段的垂直平分线上。
41.线段的垂直平分线可看作和线段两端点距离相等的所有点的集合。
42.定理1：关于某条直线对称的两个图形是全等形。
43.定理2：如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线。
44.定理3：两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上。
45.逆定理：如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称。
46.勾股定理：直角三角形两直角边a、b的平方和、等于斜边c的平方，即a^2+b^2=c^2。
47.勾股定理的逆定理：如果三角形的三边长a、b、c有关系a^2+b^2=c^2 ，那么这个三角形是直角三角形。
48.定理：四边形的内角和等于360°。
49.四边形的外角和等于360°。
50.多边形内角和定理：n边形的内角的和等于(n-2)×180°。
51.推论：任意多边的外角和等于360°。
52.平行四边形性质定理1：平行四边形的对角相等。
53.平行四边形性质定理2：平行四边形的对边相等。
54.推论：夹在两条平行线间的平行线段相等。
55.平行四边形性质定理3：平行四边形的对角线互相平分。
56.平行四边形判定定理1：两组对角分别相等的四边形是平行四边形。
57.平行四边形判定定理2：两组对边分别相等的四边形是平行四边形。
58.平行四边形判定定理3：对角线互相平分的四边形是平行四边形。
59.平行四边形判定定理4：一组对边平行相等的四边形是平行四边形。
60.矩形性质定理1：矩形的四个角都是直角。
61.矩形性质定理2：矩形的对角线相等。
62.矩形判定定理1：有三个角是直角的四边形是矩形。
63.矩形判定定理2：对角线相等的平行四边形是矩形。
64.菱形性质定理1：菱形的四条边都相。
65.菱形性质定理2：菱形的对角线互相垂直，并且每一条对角线平分一组对角。
66.菱形面积=对角线乘积的一半，即s=(a×b)÷2
67.菱形判定定理1：四边都相等的四边形是菱形。
68.菱形判定定理2：对角线互相垂直的平行四边形是菱形。
69：正方形性质定理1:：正方形的四个角都是直角，四条边都相等。
三、易错知识点大盘点
三、易错知识点大盘点
1.分母不能为0；自然数包括0。
2.集合考虑到空集。
3.求二次项系数时，注意是否有负号。
4.形如ax2+bx+c=0，注意：
①△的正负和0值
②a是否为0
③ax2+bx+a=0时，x1*x2=1
5.负数没有几何平均数；题目未说明x、y的正负，慎用均值不等式；注意几何平均值和均值不等式在公式上的区别。
6.最大公约数和最小公倍数应用在植树问题时，“+1”的问题要注意。
7.注意题干的物体可能隐藏“不可分割性”即整除性这一特性。
8.当有的选项有两个值、而别的选项只有一个值时，注意所算的情况是否有漏、有重复。
9.觉得一道题晦涩难懂时，将文字语言转化为数字语言，找到相应的知识点和考点。
10.注意题干所给的细节条件，比如出现“x为自然数”，可能要用到x的非负性、整除性，又比如“a、b、c是△的三边”，可能要用到a+b＞c的性质，从细节入手解题也可以变得更高效。
11.条件（方程）个数≥未知数个数，且各条件（方程）之间不存在放大缩小关系，此时未知数不能全部解出。
12.求最值或取值范围时，想到：
①韦达定理
②均值不等式
③三角不等式（题目有绝对值）
13.等比数列注意q=1的情况，等差数列注意常数数列。
14.不管等差还是等比，数列注意n=1和n≥2时数列是否一致。
15.注意“增加了”和“增加至”的区别。
16.截距有正负。
17.平面几何一次函数注意平行于x、y轴的情况，即斜率不存在。
18.x2+y2+Dx+Ey+F=0想成为圆，要D2+E2-4F＞0。
19.(x,y)关于(a,b)的对称点为（2a-x,2b-y），Ax+By+C=0关于（a,b）对称点为A（2a-x）+B（2b-y）+C=0。
20.题干有未知数，而选项为常数，考虑特殊值。
21.注意分房和分组的区别：有“每个位置至少一个”是分组，没有的则是分房。
22.看到x+y=1时，想到：
①整体代入
②y=1-x；
看到x+y=0时，想到：
y=-x；
看到xy=1时，想到：
①整体代入
②y=1/x
23.根号二≈1.414；根号三≈1.732；根号五≈2.236。
24.充分性判断：
①题干直接写了a=x,b=y，思考可不可以a=y,b=x
②两个条件存在互补，联合后看看有没有反例；两个条件分别独立思考，小心潜意识下的联合
③有的题目看着是要联合，但其实单个就能推出题干结论。
微信公众号
微博二维码